https://codeforces.com/blog/entry/72330
위 에디토리얼과 그 댓글들을 참조했습니다.
<교차하는 모든 선분 쌍에 대한 처리>

이런 선분들이 있을 때, 교차하는 선분 쌍 (u,v), (v,w)를 만들 수 있는 방법에 대해 소개하고자 한다. 쉬울 것 같지만 필자 기준으로 이해하는 데 상당한 시간이 걸렸다.
1. 각 정점의 양 끝점을 P a[MAX]에 담아둔다.
2. vector<P> evs에 (a[i].first, i) 와 (a[i].second, i)를 모두 담아서 오름차순 정렬한다.
3. set<P> cand를 마련한다. (아직 교차할 정점을 찾을 여지가 남은 정점의 (우측끝점, 정점번호)를 기억해 두기 위함.)
4. 정렬해둔 evs를 차례로 순차하면서 ( evs는 선분이 아닌, 선분에 속한 끝점과 그 선분의 번호를 의미함에 주의 )
4-1. cand에 p가 있는 경우 cand에서 p를 지운다.
(이제 p가 가리키는 정점은 더이상 교차할 정점을 찾을 리 없으므로)
4-2-1. cand에 p가 없는 경우 p는 어떤 선분의 시작점이다. 일단 p가 속한 정점(u = p.second)의 시작점(lu) 끝점(ru)을 마련해둔다.
4-2-2. cand를 차례로 순차하면서, ( for(P q : cand) ) q가 속한 정점(v = q.second)의 우측끝점이 u의 우측끝점보다 작을 때에 u와 v는 교차한다고 할 수 있다.
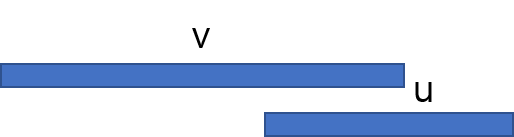
4-2-3. rv가 ru보다 커지는 시점이후는 더이상 봐줄 필요가 없다 (u가 v에 포함되므로)

아래와 같은 상황은 4-1에서 해결했기 때문에 일어나지 않는다!

위 알고리즘의 시간복잡도는 $O(n^2\times(logn))$ 정도로, 대부분의 문제에 그대로 적용하기에 문제가 있다. 아래 코드를 살짝 변형해서 풀거나, 접근 자체를 다르게 해야 한다.
<코드>
int main(){
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i].first >> a[i].second; // 선분의 양 끝점을 pair a배열에 저장
vector<P> evs;
for (int i = 0; i < n; i++) {
evs.push_back({ a[i].first,i });
evs.push_back({ a[i].second,i });
}
sort(evs.begin(), evs.end());
set<P> cand;
int cnt = 0;
for (P p : evs) { //p가 우측끝점인 경우 p가 속한 선분은
if (cand.count(p)) cand.erase(p); //더이상 다른 선분과 교차할 여지가 없음
else {
int u = p.second; //선분의 좌측끝점을 담은 p만 이 블럭으로
int lu = a[u].first, ru = a[u].second; //(참고) {ru,u}는 evs에서 아직 처리하지 않음
for (P q : cand) { //q는 다른 선분과 교차할 여지가 있는 선분에 속한 우측 끝점을 의미.
int v = q.second; //set에서 순차로 꺼내기 때문에 우측 끝점이 작은 순서대로 꺼내짐
int lv = a[v].first, rv = a[v].second;
if (rv > ru) break; //u가 v에 포함되는 경우 break;
//이곳에 진입하는 u, v는 서로 교차한다.
}
cand.insert({ ru, u });
}
}
}
<문제>
https://codeforces.com/contest/1278/problem/D
Problem - D - Codeforces
codeforces.com
<문제설명>


왼쪽과 같은 선분들이 주어지면 우측과 같은 그래프를 형성한다고 하자.
주어진 선분들이 트리를 이루는지 판단하는 문제다.
<풀이>
위에서 설명한 코드에서 u,v가 쌍을 이루는 부분에 정확히 n-1번 진입하고, 모든 정점들이 하나 이상의 간선에 포함된다면 그 그래프는 트리를 이룬다.
<코드>
int n;
P a[N];
vector<int> adj[N];
bool used[N];
void dfs(int curr, int prev = -1) {
used[curr] = true;
for (int next : adj[curr]) {
if (next == prev || used[next]) continue;
dfs(next, curr);
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i].first >> a[i].second;
vector<P> evs;
for (int i = 0; i < n; i++) {
evs.push_back({ a[i].first,i });
evs.push_back({ a[i].second,i });
}
sort(evs.begin(), evs.end());
set<P> cand;
int cnt = 0;
for (P p : evs) {
if (cand.count(p)) cand.erase(p);
else {
int u = p.second;
int lu = a[u].first, ru = a[u].second;
for (P q : cand) { //min-heap, 기준
int v = q.second;
int lv = a[v].first, rv = a[v].second;
if (rv > ru) break;
adj[u].push_back(v);
adj[v].push_back(u);
cnt++;
if (cnt >= n) break;
}
cand.insert({ ru, u });
}
}
dfs(0);
if (cnt == n - 1 && count(used, used + n, 1) == n) {
cout << "YES\n";
}
else {
cout << "NO\n";
}
}
