https://www.acmicpc.net/problem/15759
세시간 시간재고 이 문제를 풀 수 있다면 이 포스팅은 건너 뛰어도 좋다.
흔히 가방문제라고 알려진 기본 dp 유형이다. 쉬운 유형이라고 생각했으나, 여러 방법으로 응용되는 문제들을 풀어보고 알게된 것들을 공유하고자 한다.
https://www.acmicpc.net/problem/12865
냅색이 뭐였는지 기억이 안난다면 위 문제를 빠르게 다시 풀어보자.
이번 포스팅으로 위 문제처럼 한 가지 물품을 단 한번 만 넣어야 하는 경우, 한 가지 물품을 여러 개 넣을 수 있는 경우, 한 가지 물품을 최대 k개 넣을 수 있는 경우, 만족도가 이상하게 정의되는 경우 등에 대해 원리를 알고 문제를 풀어보려고 한다.
1차원으로 짤 수 있다고 해도, 2차원 점화식이 세워지는 것을 이해하고 dp 테이블을 채울 수 있는지 점검해보자.
결론부터 말하자면 보통의 경우 냅색문제는 재귀를 사용하지 않는 것이 훨씬 유리하다. 시간복잡도 자체가 다르게 나올 여지도 있고 공간복잡도 면에서도 불리하다. 또한 식을 이해만 한다면 가독성면에서도 for문을 사용하는 것이 좋다. 하지만 아직 for문으로 짜는 것을 이해하지 못한 상황이라면 일단 재귀로 풀어보고 따라와 주면 좋겠다.
<문제1>
https://cses.fi/problemset/task/1636
CSES - Coin Combinations II
cses.fi
https://www.youtube.com/watch?v=DJ4a7cmjZY0
- 참고했던 영상설명. 조회수가 4만이 넘는다. 웰노운 중 기본
<문제설명>
서로 다른 동전의 가치가 최대 100개 주어질때, 이 동전을 이용해서 정확하게 x원을 사용하는 경우의 수를 구해라. 각 동전은 무한히 사용할 수 있다. (단, 예를들어, 11원을 만들고자 할 때, 2 2 2 5와 5 2 2 2 는 같은 경우로 친다)
**구현까지 30분 시간재고 풀어보자**
+바텀업으로 짠 경우 탑다운 점화식을, 탑다운으로 짠 경우 바텀업 점화식까지만 써보자.
(서두에서 준 문제와 같이 쉬운 문제만 푼 경우, 이 문제가 좀 어색하게 느껴질 수 있다. 서두에서 준 문제는 버틸 수 있는 무게한도 내에서 최대값이고, 이 문제는 정확하게 x원을 만들어내는 경우의 수이다. 구분해서 생각해보자.)
(이 문제는 애초에 for문으로만 돌아가도록 제한이 걸려있다. 재귀로 짠 경우 런타임에러가 뜰 것. 돈 제한을 1e5로 줄인 후 1,3,6,7테스트케이스만 맞춰보자.)
<2차원 dp 풀이>
이를테면, 11원을 만들 때 {2,2,2,5}를 선택하는 경우와 {5,2,2,2}를 선택하는 경우를 중복해서 세지 않도록 동전의 순서를 강제해야 한다.
(재귀)
f(k,i) = i번째 이후의 동전을 순서대로 사용해서 k원을 만드는 경우의 수
= i번째 동전을 0번, 1번, 2번,,,,,j번 사용한 모든 경우의 수의 합

(재귀 코드)
const int MAX = 1e5;
const int MOD = 1e9 + 7;
ll n, x, dp[MAX][101], c[101];
//k원 만드는 데 i번째 이후의 동전을 사용해서 만드는 경우의 수
ll f(int k, int i) {
// if (k < 0) return 0; ..이런경우는 생기지 않도록 점화식 조정
if (k == 0 && i == n) return 1; //가능한 경우
else if (i == n) return 0; //불가능한 경우
ll& ret = dp[k][i];
if (ret != -1) return ret;
ret = 0;
for (int cnt = 0; cnt*c[i] <= k; cnt++) {
ret += f(k - c[i] * cnt, i + 1);
ret %= MOD;
}
return ret;
}
int main() {
FAST; cin >> n >> x;
for (int i = 0; i < n; i++) cin >> c[i];
memset(dp, -1, sizeof(dp));
cout << f(x, 0) << '\n';
}시간복잡도는 대충 O(k^2*i)에서 O(k*루트(k) * i)정도 나온다. 엥? 너무 큰거아니냐? 맞다. 이런 케이스 때문에 냅색은 보통 재귀로 짜는 거 아니다.
(for문)
f(k, i) = k원을 만드는데 0~i번째 동전을 순서대로 사용해서 만드는 경우의 수.
= f(k-a[i], i) + f(k, i-1) : 마지막으로 i번째 동전을 사용하거나, 사용하지 않거나
위 점화식이 당연해 보여도, 직접 테이블을 그려보면 정말 도움된다. https://www.youtube.com/watch?v=DJ4a7cmjZY0
귀찮아도 이 동영상보면서 dp테이블 직접 그려보자. 꼭 그려보세요. 그려보면 1차원 dp식이 이해될 것.
(for문 코드) .. 사이트가 이상해서 밑 코드는 tle나고 d[MAX][101] -> d[101][MAX]로 바꾼 코드는 통과한다.
const int MAX = 1e6 + 2;
const int MOD = 1e9 + 7;
int n, x, a[101], dp[MAX][101]{ 0 };
int main() {
FAST;
cin >> n >> x;
for (int i = 1; i <= n; i++) cin >> a[i];
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= x; j++) {
if (a[i] <= j) dp[j][i] = (dp[j - a[i]][i] + dp[j][i - 1]) % MOD;
else dp[j][i] = dp[j][i - 1];
}
}
cout << dp[x][n] << '\n';
}
<1차원 dp 풀이 + a>
테이블이 채워지는 그림을 머리에 떠올려보면 자연스러울 것.
const int MAX = 1e6 + 2;
const int MOD = 1e9 + 7;
int n, x, a[101], d[MAX]{ 0 };
int main() {
FAST;
cin >> n >> x;
for (int i = 0; i < n; i++) cin >> a[i];
d[0] = 1; //공집합
for (int i = 0; i < n; i++)
for (int j = 1; j <= x; j++)
if(a[i]<=j) d[j] = (d[j] + d[j - a[i]]) % MOD;
cout << d[x] << '\n';
}
문제 조건을 바꿔서, 동전을 최대한 한번 사용 가능하다고 하면 테이블을 뒤에서부터 채워주면 된다.
const int MAX = 1e6 + 2;
const int MOD = 1e9 + 7;
int n, x, a[101], d[MAX]{ 0 };
int main() {
FAST;
cin >> n >> x;
for (int i = 0; i < n; i++) cin >> a[i];
d[0] = 1; //공집합
for (int i = 0; i < n; i++)
for (int j = x; j >= 0; j--)
if(a[i]<=j) d[j] = (d[j] + d[j - a[i]]) % MOD;
cout << d[x] << '\n';
}
여기까지 이해했다면 다음 문제를 풀어보자.
https://www.acmicpc.net/problem/7579
풀이 : https://suuntree.tistory.com/193
<문제2>
https://www.acmicpc.net/problem/15759
유사코골드 플2
<문제설명>
최대 250마리의 소 n마리와 최대 1000의 무게제한W가 주어진다.
각각의 소는 최대 1e6의 무게w와 최대 1e3의 능력t가 주어진다.
소들을 적절히 골라서 무게합이 W이상인 집합 중, 능력합/무게합의 최대값을 x라고 할 때, 1000x의 소수점을 버린 값을 구하라.
힌트
1000x에 대해 이분탐색
<풀이>
고른 소들의 집합을 S라고하면 무게합은 W이상이고 다음을 만족해야 한다.
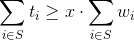
구해야 할 값은 1000x이므로 이를 y로 치환해서 다시 정리해 보면 다음과 같다.
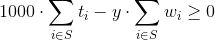
y값 1~250*1000*1000범위에 대해 이분탐색하면 된다.
int pos(y) : 능력합/무게합이 y가 가능한지?
dp[k] : 무게 합이 k일 때 1000T - yW의 최대값
dp[W] : 무게합이 W이상일 떄 1000T - yW의 최대값
dp[W]>=0이면 가능하고, 그외엔 불가능하다.
<코드>
const int MAX = 1001;
const ll INF = 1e9;
ll n, W, dp[MAX];
P a[255];
bool pos(ll k) {
fill(dp, dp + MAX, -INF);
dp[0] = 0;
for (ll i = 0, w, t; i < n; i++) {
tie(w, t) = a[i];
ll temp = 1000 * t - k * w;
for (ll j = W; j >= 0; j--) {
if (dp[j] == -INF) continue;
dp[min(W, j + w)] = max(dp[min(W, j + w)], dp[j] + temp);
}
}
return dp[W]>=0;
}
int main() {
FAST; cin >> n >> W;
for (int i = 0; i < n; i++) cin >> a[i].first >> a[i].second;
ll lo = 1, hi = 250*1000*1000+1;
while (lo < hi) {
int mid = (lo + hi+1) / 2;
if (pos(mid)) lo = mid;
else hi = mid - 1;
}
cout << lo << '\n';
}'algorithm' 카테고리의 다른 글
| 이중 연결 요소(BCC), 단절점, 단절선 (0) | 2020.05.10 |
|---|---|
| Euler Tour Tree(ETT) (0) | 2020.03.29 |
| Tree DP (1) | 2020.02.19 |


